Synopsis

#include <boost/math/quadrature/wavelet_transforms.hpp>

namespace boost::math::quadrature {

template<class F, typename Real, int p>
class daubechies_wavelet_transform
{
public:
    daubechies_wavelet_transform(F f, int grid_refinements = -1, Real tol = 100*std::numeric_limits<Real>::epsilon(),
    int max_refinements = 12) {}

    daubechies_wavelet_transform(F f, boost::math::daubechies_wavelet<Real, p> wavelet, Real tol = 100*std::numeric_limits<Real>::epsilon(),
    int max_refinements = 12);

    auto operator()(Real s, Real t)->decltype(std::declval<F>()(std::declval<Real>())) const;

};
}

The wavelet transform of a function f with respect to a wavelet ψ is

For compactly supported Daubechies wavelets, the bounds can always be taken as finite, and we have

which also defines the s=0 case.

The code provided by Boost merely forwards a lambda to the trapezoidal quadrature routine, which converges quickly due to the Euler-Maclaurin summation formula. However, the convergence is not as rapid as for infinitely differentiable functions, so the default tolerances are modified.

A basic usage is

auto psi = daubechies_wavelet<double, 8>();
auto f = [](double x) {
    return sin(1/x);
};
auto Wf = daubechies_wavelet_transform(f, psi);

double w = Wf(0.8, 7.2);

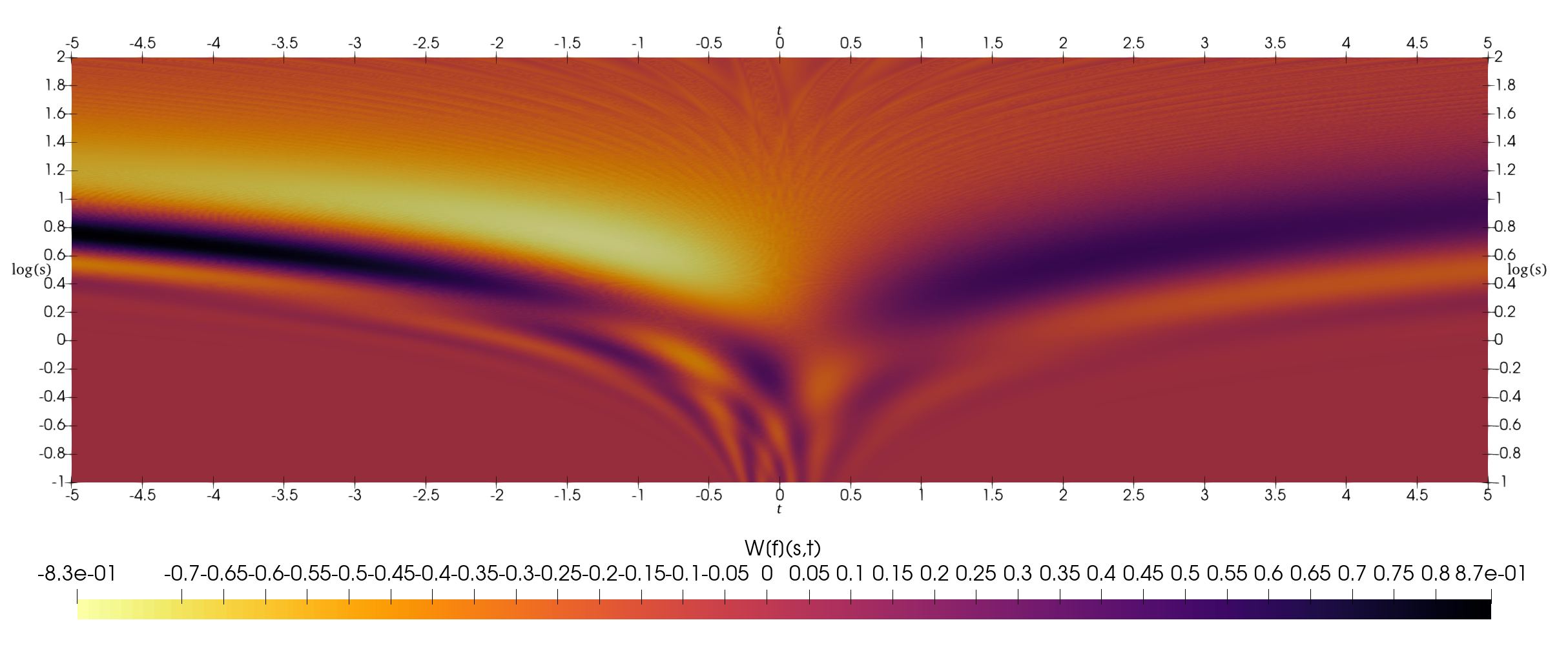
An image from this function is shown below.